Quantum computing uses quantum mechanics to process and store information in a way that is different from classical computers. While classical computers rely on bits like tiny switches that can be either 0 or 1, quantum computers use quantum bits (qubits). Qubits are unique because they can be in a mixture of 0 and 1 simultaneously – a state referred to as superposition. This unique property enables quantum computers to solve specific problems significantly faster than classical ones.
In a recent publication in EPJ Quantum Technology, Le Bin Ho from Tohoku University’s Frontier Institute for Interdisciplinary Sciences has developed a technique called “Time-dependent Stochastic Parameter Shift” in the realm of quantum computing and quantum machine learning. This breakthrough method revolutionizes the estimation of gradients or derivatives of functions, a crucial step in many computational tasks.
Typically, computing derivatives requires dissecting the function and calculating the rate of change over a small interval. But even classical computers cannot keep dividing indefinitely. In contrast, quantum computers can accomplish this task without having to discrete the function. This feature is achievable because quantum computers operate in a realm known as “quantum space,” characterized by periodicity, and no need for endless subdivisions.
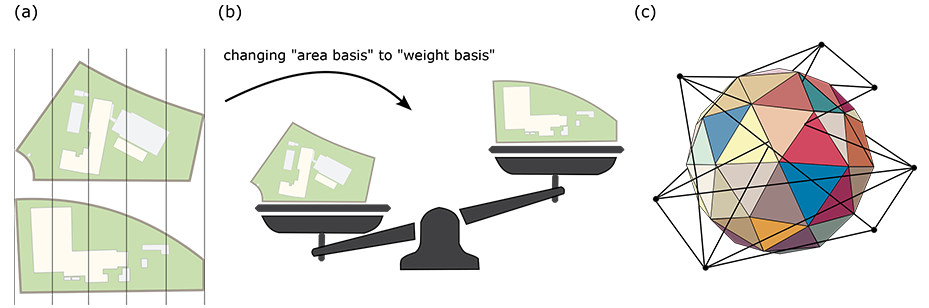
One way to illustrate this concept is by comparing the sizes of two elementary schools on a map. To do this, one might print out maps of the schools and then cut them into smaller pieces. After cutting, these pieces can be arranged into a line, with their total length compared (see Figure 1a). However, the pieces may not form a perfect rectangle, leading to inaccuracies. An infinite subdivision would be required to minimize these errors, an impractical solution, even for classical computers.
A more straightforward method involves weighing the paper pieces representing the two schools and comparing their weights (see Figure 1b). This method yields accurate results when the paper sizes are large enough to detect the mass difference. This bears resemblance to the parameter shift concept, though operating in different spaces that do not necessitate infinite intervals (as shown in Figure 1c).
“Our time-dependent stochastic method is applicable to the broader applications for higher-order derivatives and can be employed to compute the quantum Fisher information matrix (QFIM), a pivotal concept in quantum information theory and quantum metrology,” states Le.
“QFIM is intricately linked to various disciplines, including quantum metrology, phase transitions, entanglement witness, Fubini-Study metric, and quantum speed limits, making it a fundamental quantity with various applications. Therefore, calculating QFIM on quantum computers can open doors to utilizing quantum computers across diverse fields such as cryptography, optimization, drug discovery, materials science, and beyond.”
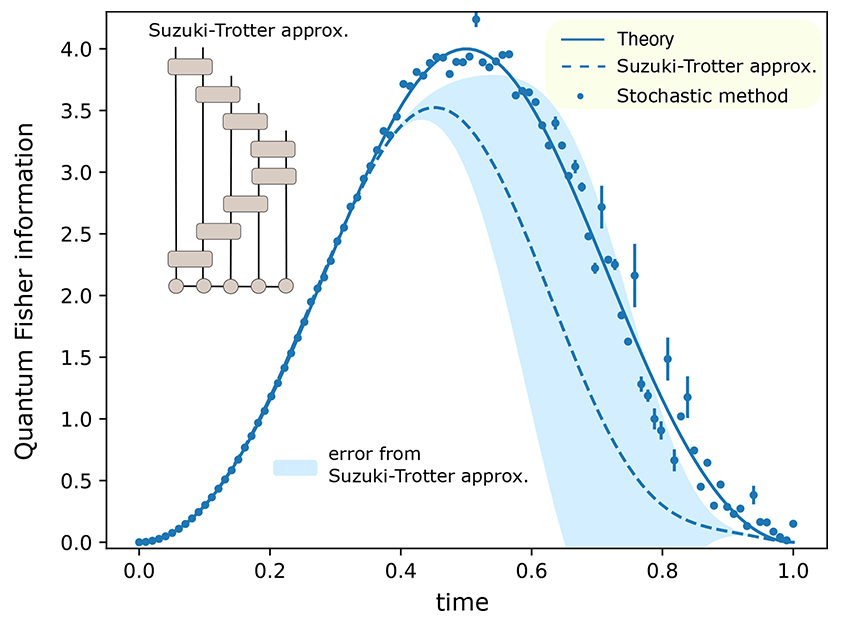
Le also showed how this method can be used in various applications, including quantum metrology with single and multiple magnetic fields and Hamiltonian tomography applied to intricate many-body systems. He also meticulously compared the new approach to the exact theoretical method and another approximation model called the Suzuki-Trotter. Although the method aligned closely with the theoretical approach, the Suzuki-Trotter approximation deviated from the true value. Enhancing the results of the Suzuki-Trotter approximation would necessitate an infinite subdivision of the Suzuki-Trotter steps.
- Publication Details:
Title: A stochastic evaluation of quantum Fisher information matrix with generic Hamiltonians
Authors: Le Bin Ho
Journal: EPJ Quantum Technology







